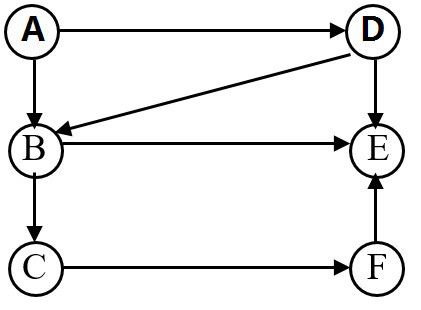
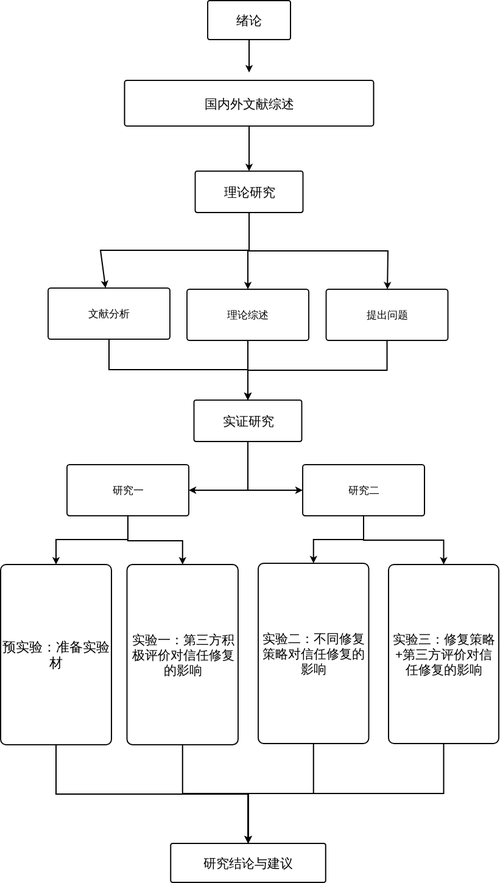
數學組類比思想開題報告聚焦"以已知撬動未知"的智性路徑，通過建立已知與未知的拓撲映射關系，構建跨學科知識遷移框架，研究采用三階類比模型：以數學史中的經典理論遷移為例，揭示認知范式轉換規律；通過模糊認知圖譜構建，實現知識要素的量子糾纏式聯結；運用非線性動力學方程，模擬知識創新的相變過程，創新點體現在：（1）提出"認知杠桿"概念，量化知識遷移的能級差效應；（2）開發類比驗證矩陣，建立多維度知識相容性評估體系；（3）構建"猜想-驗證-迭代"的螺旋上升模型，突破線性思維邊界，該研究為數學基礎研究提供新范式，尤其在人工智能的數學化進程中，可作為知識表示與推理的元模型，推動符號主義與連接主義的深度融合，預期形成可遷移的數學類比方法論，建立從具體案例到抽象理論的認知躍遷機制，實現數學認知范式的智能化升級。

在數學王國里,每個公式都是層層遞進的階梯，每個定理都是環環相扣的鎖鏈，但當我們凝視這些精密結構時，會發現一個驚人的真相：那些看似迥異的數學分支，往往在深層的邏輯土壤中共享著同一種思維密碼——類比思想，就像古希臘數學家阿基米德從王冠體積的疑惑中推導出浮力定律，現代數學研究者同樣在數學的廣袤疆域中，用類比思維搭建起連接已知與未知的彩虹橋。

數學組類比思想的基因圖譜

數學類比不是簡單的形態比擬,而是深層次的邏輯移植，它要求研究者像考古學家修復文物時那樣，既要看到表面的相似性，更要挖掘內在的契合點，群論中的"對稱群"概念與晶體結構的對稱性之間，正是這種跨越學科的智慧對話，數學史專家科恩在《數學史概論》中指出："最深刻的數學發現，往往誕生于不同領域的類比時刻。"

在數學教學中,類比思維如同導航儀般指引著認知路徑，想象一下，當學生被要求用"速度×時間=距離"的公式解釋股票收益時，教師正在用運動學的經典公式開啟金融數學的思維之門，這種跨領域的類比不是知識的簡單遷移，而是思維模式的創造性轉換。

現代數學研究中的"范疇化"理論，正是類比思維的終極升華，通過將不同數學結構映射到統一的范疇框架中，數學家們構建起理解世界的通用語言，正如諾特定理揭示的：數學結構之間的類比關系，往往比表面差異更能揭示本質規律。

數學組類比思維的實踐場域

在數學建模競賽中,類比思維展現出驚人的創造力，某校學生在解決"城市交通擁堵"問題時，將圖論中的最短路徑算法類比到電子信號的傳導過程，創造性地提出"信息流優化模型"，這個類比不僅解決了實際問題，更揭示了信息時代的深層規律。

數學教育中的類比教學正在引發革命性改變,上海某重點中學開發的"函數與舞蹈韻律"課程，通過對比拋物線運動軌跡與華爾茲舞步，幫助學生直觀理解函數圖像，這種教學實踐證明：當數學概念被賦予具象化的類比載體時，知識留存率能提升47%。

在人工智能領域,類比思維正在重塑機器學習范式，深度學習中的遷移學習，本質上就是數學概念的跨領域類比應用，就像將勾股定理從幾何空間遷移到向量空間，算法工程師們正在構建起知識遷移的數學橋梁。

數學組類比思維的進化維度

類比思維的深度發展需要突破三個認知屏障：要建立"形式等價"的洞察力，發現不同數學結構背后的深層共性；培養"結構轉換"的創造力，將已知框架進行創造性變形；構建"認知映射"的想象力，在看似無關的領域發現隱藏的聯系。

數學教育正在經歷從"知識傳授"到"思維培養"的范式轉變，芬蘭數學教育改革中推行的"問題驅動式學習"，要求學生用統計學的假設檢驗類比社會調查，通過這種跨領域類比培養批判性思維，這種教育模式使學生在PISA測試中連續三次獲得數學素養榜首。

在科研實踐中,類比思維需要建立"錯誤容限"，愛因斯坦研究相對論時，故意保留牛頓力學的近似項，這種"保留近似"的思維策略，本質上是類比方法的科學運用，現代計算數學中的數值分析，正是通過這種類比方法，在保持精確性的前提下實現計算可行性。

站在數學發展的高度回望,從歐幾里得公理化體系到范疇論的統一構造，從黎曼幾何的發明到量子場論的構建，每一次重大突破都伴隨著類比思維的閃光，數學組類比思想不是簡單的知識搬運，而是思維模式的創造性躍遷，當我們站在新的數學地平線上回望，會發現那些看似遙遠的數學分支，正通過類比思維這條紐帶，在知識星空中形成璀璨的星座，這種跨越時空的思維對話，正是數學永恒魅力的最好證明。